Friction Factor for Stainless Steel Pipe

The friction factor for stainless steel pipes is a critical parameter when designing and analyzing fluid flow systems. It plays a vital role in determining pressure losses and optimizing system efficiency. The friction factor influences the overall performance of piping systems, especially when dealing with high-velocity flows or varying fluid types. For stainless steel, which is commonly used in industries like construction, chemical processing, and water treatment, understanding the friction factor is essential for effective system design.

1. Introduction: Importance of Friction Factor in Fluid Flow

In fluid mechanics, the friction factor represents the resistance to flow within a pipe, which is affected by the material, roughness, and flow conditions. For stainless steel pipes, the friction factor is determined by both the pipe's internal surface roughness and the Reynolds number, which characterizes the flow regime (laminar, transitional, or turbulent). Accurate friction factor calculation ensures that fluid transport systems are designed to operate efficiently, minimizing energy loss and maintaining performance.

2. The Role of Friction Factor in Pipe Design

The friction factor is pivotal in calculating pressure drops and head loss in piping systems. This factor is essential for engineers when selecting pipe sizes, pump capacities, and system configurations. In stainless steel pipes, the friction factor can be influenced by various factors such as the pipe's surface finish, diameter, length, and the characteristics of the fluid being transported.

3. Factors Affecting the Friction Factor for Stainless Steel

Several factors can influence the friction factor in stainless steel pipes, including:

Surface Roughness: The roughness of the pipe’s internal surface directly impacts the friction factor. While stainless steel has a smoother surface than many other materials, it still has a characteristic roughness that affects the flow.
Flow Velocity: The friction factor varies with the velocity of the fluid. At low velocities, flow may be laminar, where the friction factor is inversely proportional to the Reynolds number. At higher velocities, the flow becomes turbulent, and the friction factor increases.
Reynolds Number: This dimensionless number characterizes the flow regime and is calculated based on fluid velocity, pipe diameter, and kinematic viscosity. It determines whether the flow is laminar, turbulent, or in transition, influencing the friction factor calculation.
Temperature and Fluid Properties: The viscosity and density of the fluid change with temperature, which in turn affects the Reynolds number and friction factor.

4. Friction Factor Calculation Methods

The friction factor for stainless steel pipes can be determined using several empirical formulas and correlations, depending on the flow regime:

Colebrook-White Equation: A widely used implicit formula that relates the friction factor to the Reynolds number and relative roughness of the pipe.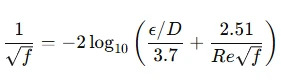

Where:

* $f$ is the Darcy-Weisbach friction factor
* $\epsilon$ is the roughness height of the pipe
* $D$ is the pipe diameter
* $Re$ is the Reynolds number

Blasius Equation: This empirical relationship is used for turbulent flow and is applicable for smooth pipes. It simplifies the calculation but is less accurate than the Colebrook-White equation for all situations.

Moody Chart: A graphical representation that helps engineers determine the friction factor for a given Reynolds number and relative roughness.

5. Laminar, Transitional, and Turbulent Flow

The flow regime plays a significant role in determining the friction factor:

Laminar Flow: Occurs at Reynolds numbers less than 2,000. The friction factor is inversely proportional to the Reynolds number.
Transitional Flow: Between Reynolds numbers of 2,000 and 4,000, the flow is unstable and difficult to predict accurately.
Turbulent Flow: Occurs at Reynolds numbers greater than 4,000. The friction factor increases as the flow becomes chaotic.

6. Practical Applications of Friction Factor in Stainless Steel Pipes

Pipeline Design: The friction factor is essential in designing pipelines for fluid transport. Accurate predictions of pressure loss are crucial for ensuring efficient pumping and minimal energy consumption.
Pump Selection: Understanding the friction factor helps in selecting pumps that can overcome pressure losses in the system.
Flow Rate Control: Engineers use friction factor calculations to design systems that maintain the desired flow rate while minimizing energy consumption.

7. Case Study: French Industrial Application

In a recent industrial application in France, a stainless steel piping system was designed for a chemical processing plant. The friction factor calculations, based on the Colebrook-White equation, helped optimize the pipe diameter and pump selection, resulting in a 15% reduction in energy consumption compared to previous systems. This case exemplifies the importance of precise friction factor calculation in industrial fluid systems.

8. Friction Factor for Different Stainless Steel Grades

Different grades of stainless steel, such as 304, 316, and duplex stainless steel, have slightly different friction factors due to their varying surface roughness. However, the differences are minimal compared to other materials like carbon steel or cast iron. The selection of the grade will mainly depend on the application environment, such as resistance to corrosion and temperature extremes.

9. Importance of Accurate Measurements

Accurate measurement of surface roughness and Reynolds number is essential for calculating the correct friction factor. Deviations from the expected values can result in suboptimal system performance, leading to increased energy consumption and potential system failures.

10. Friction Factor in Different Fluid Systems

Water and Oil: Water has a lower viscosity than oil, which results in different friction factor values. Oil-based systems may require more energy to pump due to higher friction losses.
Slurry Transport: The friction factor in slurry transport systems, which involve suspensions of solids in liquids, is higher due to the additional resistance from the solid particles.

11. Friction Factor and Energy Efficiency

Understanding the friction factor is key to improving the energy efficiency of fluid transport systems. By minimizing friction losses, engineers can design systems that require less energy to move the fluid, reducing operating costs and environmental impact.

12. Conclusion: Optimizing Stainless Steel Pipe Systems

In conclusion, the friction factor is an essential consideration when designing fluid transport systems using stainless steel pipes. Accurate calculation of this factor allows engineers to optimize system performance, minimize energy loss, and ensure long-term reliability. By applying the correct formulas and accounting for factors like surface roughness and Reynolds number, engineers can create more efficient and cost-effective systems.

Frequently Asked Questions (FAQs)

1. What is the standard formula for calculating the friction factor in stainless steel pipes?
The Colebrook-White equation is commonly used for calculating the friction factor, which takes into account both the Reynolds number and the relative roughness of the pipe.
2. How does surface roughness affect the friction factor?
A rougher pipe surface increases the friction factor, leading to higher energy consumption and pressure losses.

3. Why is the Reynolds number important in determining the friction factor?
The Reynolds number indicates the flow regime (laminar, transitional, or turbulent) and directly influences the friction factor calculation.

4. Can the friction factor be different for various grades of stainless steel?
Yes, different stainless steel grades have varying surface roughness, which can slightly affect the friction factor.

5. How can engineers reduce friction losses in stainless steel piping systems?
Engineers can reduce friction losses by selecting the appropriate pipe diameter, minimizing surface roughness, and optimizing flow velocity.

Authoritative References

Industry news

Friction Factor for Stainless Steel Pipe